You're about to create your best presentation ever

Get started with Prezi

Sample Flow Chart Template Powerpoint

Create your presentation by reusing a template from our community or transition your PowerPoint deck into a visually compelling Prezi presentation.

Powerpoint sample

Transcript: LIVING SOCIAL CHRISTMAS Living the Life in GOLD VANGIE 05 - 07

Sample powerpoint!

Transcript: On your toes Straight arms Angle to Target How to Pass a Volleyball How to not pass a volleyball HAVE A BACK-UP PLAN!! (email, thumb drive) Practice with your visual aid!! You need to be on your toes, with your arms ready for a ball to come at you at about 60 miles an hour. Then the ball must hit your forearms, and be angled to the target (The setter) The primary passer on the team is the libero. You can also be a defensive specialist! Your job is to get a great pass so that your team can run their offense. REMEMBER... Sample prezi

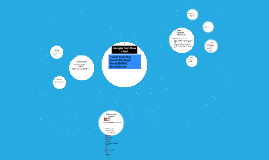
Sample Test Flow Chart

Transcript: If p-value <= alpha (default is .01) reject H0 If normal: t.test(column1, column2, alternative= "two.sided", paired=TRUE) *test mu=median z1=c(3.9,1.4,4.1,5.5,2.3) z2=c(5.4,2.0,4.8,3.8,3.5) z3=c(1.3,.7,2.2,NaN, NaN) shapiro.test(z1) shapiro.test(z2) shapiro.test(z3) Z=c(z1,z2,z3) f=c("Treatment 1", "Treatment 2", "Treatment 3") k=3 n=5 tm=gl(k, 1, n*k, factor(f)) tm av=aov(Z~ tm) summary(av) Z-test t.test(x,y, alternative="two.sided", mu=, var.equal=TRUE) Step 1: z-test (n>30) z.test( ) t-test (n<=30) t.test( ) v>.05, pooled Two Sample (Not Normal) r-code: wilcox.test(x,y, alternative=,mu=) p-value > 0.05 ~ normal (fail to reject H0) p-value<= 0.05 ~ not normal (reject H0) If both are normal and n>30, then If: If all p-values> 0.05 z.test(x,y, alternative="two.sided", mu=, sigma.x=,sigma.y=, conf.level=.95) v=var.test(x,y) One Sample If p-value <= alpha (default is .01) reject H0 *two.sided, greater, less than If: at least one column is not normal, use Wilcox test there is correlation between two columns AND both are normal, then use paired t-test at least one column has n<30 and both are normal, then use 2 sample t-test both of the columns has n>30, then use z-test. r-code: kruskal.test(data not normal) ✳✱* Check both columns for normality Two Sample (Normal) *Install Teaching Demos Package, library(BSDA), library(mass) If v<.05, unpooled Sample Test Flow Chart *sigma.x= sd(x) sigma.y= sd(y) Test the Median *dnn=data not normal dn= data normal shapiro.test( ) If at least one shapiro.test: p-value <=0.05 Step 0: Check normality If p-value >alpha, fail to reject H0 If p-value > alpha (default is .01) reject H0 t.test(x,y, alternative="two.sided", mu=) Normal Distribution If p-value > alpha (default is .01) fail to reject H0 T-test Paired T-Test If not normal, sign.test(dnn-dn) Not Normal Three or more samples sign.test(data set, md=0, alternative= "two.sided", conf.level= 0.95 ) If p-value <=alpha, reject H0 shapiro.test(x) shapiro.test(y) shapiro.test(z)

Falco Laser Flow chart template

Transcript: Laser Advance | Stay | Retreat Make a read Make a read Make a read Advance | Stay | Retreat Advance | Stay | Retreat Advance | Stay | Retreat Read the type of aproach Read more Projectile | Airial | Empty Projectile | Airial | Empty Read more Read Read Action Read Action Read Smash | Grab | Dash | Take the Hit | Shine | Power Shield Take the Hit | Shine | Intercept Nair | Fair | Dair Bair | Up Air Nair | Fair | Dair Bair | Up Air Projectile | Airial | Empty Projectile | Airial | Empty Read Read Action Action Read the type of aproach Take the Hit | Shine | Power Shield Take the Hit | Shine | Intercept Nair | Fair | Dair Bair | Up Air Nair | Fair | Dair Bair | Up Air Read more Dash Attack | Grab Special | JC Upsmash Wavedash | Dash Back Projectile | Airial | Empty Projectile | Airial | Empty Short Hop | Full Hop | Dash | Walk Wave Dash | F Smash | Special Read more Read Read Action Read Action Read Smash | Grab | Dash | Take the Hit | Shine | Power Shield Take the Hit | Shine | Intercept Nair | Fair | Dair Bair | Up Air Nair | Fair | Dair Bair | Up Air Read more Projectile | Airial | Empty Projectile | Airial | Empty Read Read Read Action Action Read Smash | Grab | Dash | Take the Hit | Shine | Power Shield Take the Hit | Shine | Intercept Nair | Fair | Dair Bair | Up Air Nair | Fair | Dair Bair | Up Air Projectile | Airial | Empty Projectile | Airial | Empty Read Read Action Action Take the Hit | Shine | Power Shield Take the Hit | Shine | Intercept Read Dash Attack | Grab Special | JC Upsmash Wavedash | Dash Back Nair | Fair | Dair Bair | Up Air Nair | Fair | Dair Bair | Up Air Read Smash | Grab | Dash | Read the type of aproach Short Hop | Full Hop | Dash | Walk Wave Dash | F Smash | Special Dash Attack | Grab Special | JC Upsmash Wavedash | Dash Back Read more Short Hop | Full Hop | Dash | Walk Wave Dash | F Smash | Special Read more Read Dash Attack | Grab Special | JC Upsmash Wavedash | Dash Back Projectile | Airial | Empty Action Projectile | Airial | Empty Read more Read Short Hop | Full Hop Dash | Walk Wave Dash | F Smash Special Read Smash | Grab | Dash | Read Read Action Read Action Read Smash | Grab | Dash | Take the Hit | Shine | Power Shield Take the Hit | Shine | Intercept Nair | Fair | Dair Bair | Up Air Projectile | Airial | Empty Projectile | Airial | Empty Nair | Fair | Dair Bair | Up Air Projectile | Airial | Empty Projectile | Airial | Empty Get in, punish Read Read Action Action Read Read Action Action Down B | Side B Up B | Neutral Take the Hit | Shine | Power Shield Take the Hit | Shine | Intercept Read Nair | Fair | Dair Bair | Up Air Nair | Fair | Dair Bair | Up Air Take the Hit | Shine | Intercept Take the Hit | Shine | Power Shield Nair | Fair | Dair Bair | Up Air Nair | Fair | Dair Bair | Up Air Read Smash | Grab | Dash | Dash Attack | Grab Special | JC Upsmash Wavedash | Dash Back Dash Attack | Grab Special | JC Upsmash Wavedash | Dash Back Short Hop | Full Hop | Dash | Walk Wave Dash | F Smash | Special Short Hop | Full Hop | Dash | Walk Wave Dash | F Smash | Special Dash Attack | Grab Special | JC Upsmash Wavedash | Dash Back Action Short Hop | Full Hop Dash | Walk Wave Dash | F Smash Special Action Read Read more Read Read Action Read Smash | Grab | Dash | Get in, punish Get in, punish Read Projectile | Airial | Empty Projectile | Airial | Empty Down B | Side B Up B | Neutral Read Read Action Action Get in, punish Take the Hit | Shine | Intercept Take the Hit | Shine | Power Shield Read Nair | Fair | Dair Bair | Up Air Nair | Fair | Dair Bair | Up Air Down B | Side B Up B | Neutral Read Smash | Grab | Dash | Dash Attack | Grab Special | JC Upsmash Wavedash | Dash Back Short Hop | Full Hop | Dash | Walk Wave Dash | F Smash | Special Dash Attack | Grab Special | JC Upsmash Wavedash | Dash Back Action Action Short Hop | Full Hop Dash | Walk Wave Dash | F Smash Special Read Read Action Down B | Side B Up B | Neutral Get in, punish Read Get in, punish Down B | Side B Up B | Neutral Get in, punish Down B | Side B Up B | Neutral Action Read Action Down B | Side B Up B | Neutral Get in, punish Read Get in, punish Down B | Side B Up B | Neutral Down B | Side B Up B | Neutral

Sample Template

Transcript: Townhall worrrmmmss June 24, 1992 Hufflepuff test Sample Template Hufflepuff test Miners and storages worrrmmmss Laboratory Barracks Barbarian King Traps Defenses Troops June 24, 1992 Kadiring movie Kadiring movie

Sample Flow Chart

Transcript: R&D will work with roving operators to find the ideal twist levels, make the correct hank roving, and score a promising CV Inspection and Shipping R&D works with winding technician to ensure strong, clean splices Retainer is taken to lab for storage Two knitdowns are done, one for lab and one for R&D's analysis/future reference If sample is carded at railroad, R&D will go over the setup with Joe and help with setup Request recieved We must keep track of the samples we send and follow up with customers to hear their thoughts and suggestions so we can continue to constantly improve Once complete, a cone will be taken to salesman and approved for shipment Max will contact the customer and inform them of the completion and arrange shipment Drawing Follow-up If carded at Clevemont, R&D will work with technician to ensure proper setup Salesman reviews request with R&D Go over details such as package size, pounds, TM, RM numbers, etc. Code is assigned, setup sheet is made, and sample is scheduled. Sample Flow Chart Patrick Yarn Mills At all processes, all setings must be recorded to ensure the ability to duplicate This includes test data, machine settings, and any special notes Release to Clevemont End Customer is notified of estimated delivery If sample is to be doubled, R&D will meet with Margarito and Danny to go over specifics such as package size, whether wax will be needed, and twist levels Once the sliver is finished, Joe will alert R&D, who then will release for transport to Clevemont. R.R. will store the cans in the designated location until release Distribution will alert R&D upon arrival of the sliver and will place in designated area Winding Max schedules S1 and S2 R&D sets up spinning frame and analyses test data All test data is recorded Roving Spinning Carding When drawing is ready to begin, R&D will approve startup. Plying/Twisting

FLOW CHART

Transcript: Location of the resources is the hard part. You must have good infrastructure for secondary activity. Proximity to markets, good infrastructure also! QUATERNARY Urban areas, good infrastructure! Infrastructure: is basic physical and organizational structures needed for the operation of a society or enterprise, or the services and facilities necessary for an economy to function ACTIVITIES of a DIAMOND PRIMARY SECONDARY TERTIARY QUATERNARY This would be a more developed society. gathering of raw materials and natural resources This is a society that is definately more developed. They have all four levels of activity. PRIMARY EX. universities, government positions, management, scientific research Tertiary would be a newly industrialized/more developed society. EX. hunting, fishing, mining SECONDARY changing natural resources into a product for consumer wants EX. steel making, textile, factories Economic Activity people prviding service; selling the product TERTIARY Primary would be a less developed society. provides info. management and reserch services by highly trained persons EX. bankers, teachers, doctors

Sample Flow

Transcript: Sample Flow Gap 1: Child's voice missing in casework TTKC engages multiple agencies, such as schools and social service agenceis, ensuring coordination of support across the board for the child social workers at the family-level have limited direct interactions with the child - unfamiliarity can contribute to a lack of rapport and a trusting relationship Although there is a social worker supporting Zixin’s family, Zixin has exhibited hesitancy in her past engagements with the social worker. Closing the presentation TTKC Sample Case Study TTKC complements SSOs by providing a trusting relationship with the child TTKC checks in with Zixin’s school counsellor concerning her future plans with Zixin and to update the social worker. Summarize each point you made Give quick call-backs so your audience remembers Make it clear this is the end TTKC remains the primary go-to for Zixin. TTKC staff checks in with her, listening to her thoughts and feelings regarding issues such as her father's discharge, while communicating information such as his new leave arrangements. Put a bold statement here Put something fun or important here Write something high-impact about this photo Use this space for details that you haven’t talked about yet. Relate what you’re saying to the nearby image so your audience has a visual, too.

Explore our templates for more presentation inspiration

Customer Stories - Office

Description: Storytelling is at the heart of great service. Use this stunning, customizable business presentation template to highlight employees who do exceptional work or position your customers as the heroes of your business.

Sales KickOff - Rocket

Description: The sky’s the limit. Boost your new sales initiative into orbit with an engaging and compelling SKO presentation. This template features a effective sales kickoff theme that makes it easy to be engaging. Like all Prezi SKO templates, it’s fully customizable with your own information.

Marketing Proposal Template for Powerful Presentations | Prezi

Description: Catch the eye and engage the imagination with this cool-looking Prezi proposal template. The bold, bright design and highly dynamic theme all but guarantee success for your next sales or marketing proposal. All Prezi presentation templates are easily customized.

Quarterly Business Review - Downtown

Description: Add some color to your quarterly business review with this vibrant business presentation template. The bold visuals in this business template will make your next QBR a memorable one.

Now you can make any subject more engaging and memorable

Get started with Prezi